Guessing better in Wordle using Python

It’s a new year and usually, people tend to make goals of working out, getting more organized, and leaving addictions, and I’m no different. But to my surprise, I started the year with a new addiction I don’t think I’ll plan to quit so soon: Wordle, that game by Josh Wardle (@powerlanguish) which was even featured in the NY Times.

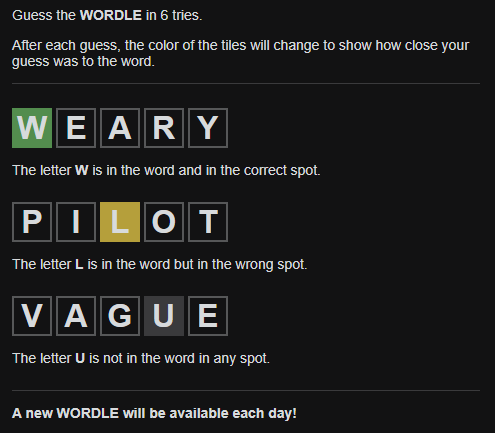
The idea of the game is pretty simple, yet, very interesting. You have 6 tries on guessing a word per day. On each guess, the game will tell which letters are in the word - in the correct spot and somewhere else in the word - and if a letter is not in the word at all. With this information you try more times, getting more information on each try, up to the 6th or earlier guess where you guesses correctly or you didn’t get it.

As you have only 6 guesses per day, this can become very serious. In the past few days, I spent about 15 or more minutes trying to solve this. With many of these minutes it was just me idling, thinking of 5 letter words in English.

But, being the curious person I am, I started wondering what would be the best approach for this. Many theories came from friends and the internet: starting with a specific word, trying to use words with non-repeating letters (even if you are already sure of a letter in a specific place), and more. But, are they right?

So I decided to take on this little challenge of getting these answers using code, more specifically, my favorite language for this kind of thing, Python. But looking back, as I wanted to test different scenarios multiple times, I should’ve tried using C++.

Disclaimer

From this point on, I’ll share pieces of code and information that can potentially be used for cheating. My idea with this was never to cheat in any way when playing (I mean, what’s the point?). I haven’t used any of the key information I got for this end, and I highly recommend you not spoil the fun either.

In case you want to play with this, I’ll be making all the code available on GitHub (link to come soon - ping me on Twitter if the link isn’t here yet and I’ll let you know when it’s ready - still cleaning it up a bit).

I’m by no means the first to think of writing a piece of code that could solve or aid the game. After having the idea some posts started to pop up on my Twitter feed, but I didn’t want to get “contaminated” and decided to bookmark those for later. After playing a lot with my solution on Python I went ahead to look at the other’s take on this. Tyler Glaeil wrote a really cool article on the mathematically optimal first guess, Rodrigo Serrão wrote a solver in python and shared it on their site, and Bertrand Fan also decided on answering what’s the best starting word in Wordle.

Word database

The first thing I did was to find a database of English words. I started with the words from swyl/english-words repository. Later, when I read Bertrand’s post, I realized I could actually use the words from the game source code. The results I’ll show here are considering the game words, but initially, I only used the words from the first source I mentioned here, which were more than enough for playing with and yield very similar results to the Wordle words.

The database is made by 2315 possible words for each day, with other 10657 words that are less common and are accepted as guesses. So, a total of 12972 words are to be used in guesses and in my experiments.

For all effects, the results I’m showing here are running the tests 1000 times, keeping the same secret words in between experiments, meaning I’ll test 1000 different words in each approach and will compare them.

Implementing the game itself

With the word database, I started to implement the game. As the game is simple, so was the code that plays it. The basic structure is like this:

def play(secret_word):
    words = get_all_words()
    for i in range(0, 6):
        guess = pick_word(words)
        result = calculate_guess(secret_word, guess)
        if all(result[i] == Result.CorrectSpot for i in range(0, len(result))):
            print(f"I got it in {number_of_guesses} tries! The secret word was: {secret_word}")
            break
        words = filter_words(guess, result, words, secret_word)

I start storing all the 5 letter words in an array words. And then, iterate 6 times picking a random word from words, calculating the result for this guess, and, if in the result all the letters are in the correct spot, then I know I won. Otherwise, I filter the words on the array with the information I got from the result.

To represent the result I used an Enum and a simple matcher to calculate the result:

class Result(Enum):
    CorrectSpot = 1
    IncorrectSpot = 2
    NoSpot = 3
    
def calculate_guess(secret_word, guess_word):
    def match_latter(secret_word, guess_word, i):
        if secret_word[i] == guess_word[i]:
            return Result.CorrectSpot
        elif guess_word[i] in secret_word:
            return Result.IncorrectSpot
        else:
            return Result.NoSpot

    return [match_latter(secret_word, guess_word, i) for i in range(0, len(secret_word))] if (len(guess_word) and len(secret_word)) else None

For each letter on the guess word, there’s a Result value: A Result.CorrectSpot if the letter in the specific position in the guess word is the same - in the same position - in the secret word. An Result.IncorrectSpot if the letter is not in the same place in the guess word, but it’s present in the word somewhere else. And Result.NoSpot if the letter is not present at all in the secret word.

def filter_words(guess_word, result, words):
    # remove the guess_word from the list of words
    words = [word for word in words if word != guess_word]

    # filter by the letters we know aren't in the secret word
    forbidden_letters = [guess_word[i] for i in range(0, len(guess_word)) if result[i] == Result.NoSpot]
    words = [word for word in words if not any(letter in word for letter in forbidden_letters)]

    # filter by the letters we know are in the secret word, in the correct spot
    for i in range(0, len(guess_word)):
        if result[i] == Result.CorrectSpot:
            words = [word for word in words if word[i] == guess_word[i]]

    # finally, filter by the letters we know should be in the word
    existing_letters = [guess_word[i] for i in range(0, len(guess_word)) if result[i] != Result.NoSpot]
    if existing_letters:
        words = [word for word in words if any(letter in word for letter in existing_letters)]

    return words

The filter is very simple. I start by removing the guess word from the words left. Then, I follow on using the information from the result, that is, removing words that have any letter that was flagged by Result.NoSpot, removing words that do not have the letters in the specific locations identified by Result.CorrectSpot, and finally, filtering out the words that don’t have any of the letters that we know are in the secret word, tagged by either Result.CorrectSpot or Result.IncorrectSpot.

With this, I was left on how to pick my guesses. My first approach was a naive and the simplest solution I could think of: randomly pick a word from the words array.

def pick_word(words):
    return random.choice(words) if words else None

With my naive solution, the program was being able to win the game 49.7% of the time, with an average of 4.1 guesses. On the losing scenarios, I got an average of 1.3 letters in the correct place found. It was kind of ok, but now the real fun begins. What I can do to increase the winning percentage?

Smart-ish solution

The first thing I wanted to try was to prefer guesses that didn’t have any duplicated letters, trying to have more information on different letters on each guess. If there is no word fitting these criteria, then I would fall back to the naive random solution.

def smartish_pick_word(words):
    good_options = [word for word in words if len(set(word)) == len(word)]
    return pick_word(good_options) if len(good_options) else pick_word(words)

With this mode, I got 66.7% of wins, with an average of 4.1 guesses. A good improvement from the 49.7% from the naive, but not as I was anticipating. I believe the reason for this is that at the end of my guesses, I was still left with an average of 12 letters in the alphabet as well as many words to try as in the losing scenarios. In the cases where it loses it only knows about 1.2 letters in the correct place. That’s why I called it smart-ish, the idea looked good at first, but not that much in practice.

Smart considering most common letters

To try to improve my implementation, I tried to use the knowledge of the most common letters in English. The idea was to keep the idea of choosing words without repetition of letters, but first, consider words that contained at least 2 of the 8 most common letters in English. If we don’t have any words fitting this, then fall back to the Smart-ish solution.

def words_with_common_letters(i, words):
    # filter words that have at least two of the 8 most common letters
    most_common_letters = ['e', 't', 'a', 'o', 'i', 'n', 's', 'r']	
    good_options = [word for word in words if len(set(word)) == len(word)]
    good_options = [word for word in good_options if (sum(1 if letter in most_common_letters else 0 for letter in word)) >= 2] if len(good_options) else []
    return smartish_pick_word(i, good_options) if len(good_options) else smartish_pick_word(i, words)

This improvement barely raised the win porcentage from the previous 66.7% using the Smart-ish solution to 66.9% wins, with an average of 4 guesses to win.

Weigthing the letters

I still had hoped of using the information on the most common letters so I decided to try this in another way. Still, with the idea of preferring words that don’t have duplicated letters, I follow on giving weights for the words. This weight is a simple function of using the frequency of each letter in the alphabet as the value for that letter in a word. For example, the letter E is the most common with a frequency of 13%, so the weight of the letter E is 13. The letter T has a frequency of 9.1%, so its weight in a word is 9.1. And so on.

def weigth_words(words):
    good_options = [word for word in words if len(set(word)) == len(word)]
    if len(good_options) == 0:
        good_options = words
    words_weigth = [(word, sum(most_common_letters[letter] for letter in word)) for word in good_options]
    words_weigth = sorted(words_weigth, key=lambda x: x[1], reverse=True)
    return words_weigth[0][0] if len(words_weigth) else words_with_common_letters(words)

When there was no good option without duplicated letters, I would still try to weight all the remaining words. And, after sorting those, I would choose the one with a higher weight.

This yield a good result, with 75% of wins, with an average of 3.7 guesses.

Avoiding any repetition at first

That’s the point where I started talking with friends to understand their approaches. One of them told me they tried to use words that didn’t have any letter in common with the previous, even if the previous one gave them some knowledge of the placement or existence of a given letter. So I wanted to try this option.

def avoid_repetitions_at_first(i, tried_words, words):
    if i < 3:
        forbidden_letters = [word[i] for word in tried_words]
        good_options = [word for word in words if not any(letter in word for letter in forbidden_letters)]
        if len(good_options) == 0:
            good_options = words
        guess = weigth_words(i, good_options)
    else:
        guess = weigth_words(i, words)

    return guess

For this, I stored all the previous guesses and removed any words that had any letter that was already used. With some tests, I saw that using this only on the first 3 tries yielded better results. Otherwise, when this is not possible - there are no words matching this - I would use the weighting method.

With this approach, I got 76% of wins, with an average of 3.8 guesses to find the correct word. Which Is not that different from weighting the letters, but in practice, for a human approach, is much easier to use.

Starting with a specific word

The last test I wanted to conduct was to see if starting with a specific word would give me better results than any of the previous attempts. This has been the most discussed thing around the game, with some saying that starting with words like “roate”, “soare”, “orate”, or even some words that don’t look like words but have a bunch of vowels like “adieu” or “aeons” will give better results. So, I want to put that under a test. I chose to stick to words that actually sound like words because in practice when playing, those are the words I usually try.

The code for this is basically forcing the first guess, and afterward falling back in the avoid repetition method, as it was the one yielding the best results so far. As I had more than 2300 words to consider, and I wanted to run each test 1000 times, this took ages to run. At this point, I regretted not watching out for performance in the code, but I was already committed and went the lazy way - multiprocessing the code.

Going by the numbers, the best word (and again, here I’m only considering words that are more common) to start the guesses is “prism”, with 83.4% of victories. But other words like “stomp”, “crisp”, “sport”, “blush”, among others were still above 82% of victories. The average number of guesses ranged from 3.7 to 3.9. In total, about 110 words being chosen as first words gave it more than 80% of the wins.

That was very interesting to see because it actually raised the percentage of wins from a previously 76% in many cases, which I was not really expecting to be that different. Also, when checking the lowest scoring words, many words with repeated letters show up, like “queue”, “jetty”, “woozy”, corroborating with the idea of prioritizing words with unique letters. These worst rating words only made about 64% of wins, with an average of 4 guesses.

The words I found in many of the articles are not considered as real-ish words by the game, in the sense they will never be answers to the daily challenges. But either way, I wanted to see how they would behave, and to my surprise, they did not that great compared to the words I found as the best ones to start. Using the word “roate” as a first guess gave 78.1% of wins, “orate”, “adieu”, “aeons” had between 77.2% and 77.6%, and “soare” only wins in 74.5% of the times.

Summary of attempts

	Naive	Smart-ish	Smart with common letters	Weighting letters	Avoiding repetitions at first	Starting with “prism”
Winning percentage	49.7	66.7	66.9	75	76	83.4
Average tries	4.1	4.1	4	3.7	3.8	3.8

Final thoughts and (possible) future work

At the end of the day, most approaches here are not practical unless you want to use a computer to solve the challenges which is basically taking out the fun of the game, but regardless, I had a lot of fun playing with the code, trying to tweak the algorithms to reach better results. There’s still quite a lot of things I would like to try, for instance, perfecting the guesses to better distribute the possible letters when using an approach like avoiding the repetition and doing a frequency and placement analysis of the letters in the possible 5 letter words instead of using the generic frequency of letters in English. My gut feeling is that with better algorithms I could reach something around 90% or higher.

Also, recently a Wordle version in Brazilian Portuguese was released and I would like to see if the same approaches for the English version would work as well in Portuguese.

Based on the not-so-great performance of some of the experiments, I would also consider redoing this in C++, just so I have a bit more room for longer and more expensive computations.

In a few weeks, given that I will not get tired of the game sooner than this, I also intend on returning to this code to see how much better or worst the algorithms are compared to my non-cheating-human-powered results. So far, for the few words I played, I’m doing much better than my best algorithm here as I haven’t got any word wrong, but yes, it’s too early to conclude I’m better than my computer.

If you got any ideas on how to improve the performance of the algorithm and would like to share, just shout out on Twitter.